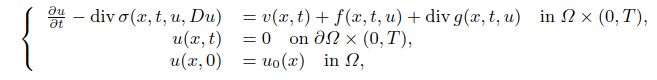An existence result for quasilinear parabolic systems with lower order terms
Abstract
In this paper we prove the existence of weak solutions for a class of quasilinear parabolic systems, which correspond to diffusion problems, in the form
where Ω is a bounded open domain of be given and
The function v belongs to
is in a moving and dissolving substance, the dissolution is described by f and the motion by g. We prove the existence result by using Galerkin’s approximation and the theory of Young measures.
Keyword : quasilinear parabolic systems, weak solutions, Young measures
How to Cite
Balaadich, F., & Azroul, E. (2021). An existence result for quasilinear parabolic systems with lower order terms. Mathematical Modelling and Analysis, 26(4), 669-683. https://doi.org/10.3846/mma.2021.13553

This work is licensed under a Creative Commons Attribution 4.0 International License.
References
F. Augsburger and N. Hungerbühler. Quasilinear elliptic systems in divergence form with weak monotonicity and nonlinear physical data. Electronic Journal of Differential Equations, 144:1–18, 2004.
E. Azroul and F. Balaadich. Weak solutions for generalized p-Laplacian systems via Young measures. Moroccan J. of Pure and Appl. Anal. (MJPAA), 4(2):77–84, 2018. https://doi.org/10.1515/mjpaa-2018-0008
E. Azroul and F. Balaadich. Quasilinear elliptic systems in perturbed form. Int. J. Nonlinear Anal. Appl, 10(2):255–266, 2019.
E. Azroul and F. Balaadich. Strongly quasilinear parabolic systems in divergence form with weak monotonicity. Khayyam J. Math., 6(1):57–72, 2020.
E. Azroul and F. Balaadich. On strongly quasilinear elliptic systems with weak monotonicity. J. Appl. Anal., 27(1):153–162, 2021. https://doi.org/10.1515/jaa-2020-2041
E. Azroul and F. Balaadich. A weak solution to quasilinear elliptic problems with perturbed gradient. Rend. Circ. Mat. Palermo II, 70:151–166, 2021. https://doi.org/10.1007/s12215-020-00488-4
J.M. Ball. A version of the fundamental theorem for Young measures. In M. Rascle, D. Serre and M. Slemrod(Eds.), PDEs and Continuum Models of Phase Transitions, volume 344, pp. 207–215, Berlin, Heidelberg, 1989. Springer Berlin Heidelberg. https://doi.org/10.1007/BFb0024945
V. Bo¨gelein, F. Duzaar, L. Scha¨tzler and C. Scheven. Existence for evolutionary problems with linear growth by stability methods. J. Differential Equations, 266(11):7709–7748, 2019. https://doi.org/10.1016/j.jde.2018.12.012
M. Caddick and E. Suli. Numerical approximation of Youngmeasure solutions to parabolic systems of forward-backward type. Applicable Analysis and Discrete Mathematics, 13(3):649–696, 2019. https://doi.org/10.2298/AADM190325026C
S. Demoulini. Young measure solutions for a nonlinear parabolic equation of forward-backward type. SIAM Journal on Mathematical Analysis, 27(2):376– 403, 1994. https://doi.org/10.1137/S0036141094261847
G. Dolzmann, N. Hungerbühler and S. Müller. Nonlinear elliptic systems with measure-valued right hand side. Mathematische zeitschrift, 226:545–574, 1997. https://doi.org/10.1007/PL00004354
L.C. Evans. Weak convergence methods for nonlinear partial differential equations. CBMS Reg. Conf. Ser. in Math., 74, 1990. https://doi.org/10.1090/cbms/074
N. Hungerbühler. A refinement of Ball’s theorem on Young measures. New York J. Math, 3:48–53, 1997.
N. Hungerbühler. Quasilinear elliptic systems in divergence form with weak monotonicity. New York J. Math., 5:83–90, 1999.
N. Hungerbühler. Quasilinear parabolic systems in divergence form with weak monotonicity. Duke mathematical journal, 107(3):497–519, 2001. https://doi.org/10.1215/S0012-7094-01-10733-3
E. Kamke. Das Lebesgue-Stieltjes-Integral. Teubner, Leipzig, 1960.
G.M. Lieberman. The natural generalizationj of the natural conditions of Ladyzhenskaya and Ural’tseva for elliptic equations. Communications in Partial Differential Equations, 16(2-3):311–361, 1991. https://doi.org/10.1080/03605309108820761
P. Marcellini. A variational approach to parabolic equations under general and p, q-growth conditions. Nonlinear Analysis, 194:111–456, 2020. https://doi.org/10.1016/j.na.2019.02.010
R. Di Nardo, F. Feo and O. Guibe. Existence result for nonlinear parabolic equations with lower order terms. Anal. Appl.(Singap.), 9(2):161–186, 2011. https://doi.org/10.1142/S0219530511001790
E. Azroul and F. Balaadich. Weak solutions for generalized p-Laplacian systems via Young measures. Moroccan J. of Pure and Appl. Anal. (MJPAA), 4(2):77–84, 2018. https://doi.org/10.1515/mjpaa-2018-0008
E. Azroul and F. Balaadich. Quasilinear elliptic systems in perturbed form. Int. J. Nonlinear Anal. Appl, 10(2):255–266, 2019.
E. Azroul and F. Balaadich. Strongly quasilinear parabolic systems in divergence form with weak monotonicity. Khayyam J. Math., 6(1):57–72, 2020.
E. Azroul and F. Balaadich. On strongly quasilinear elliptic systems with weak monotonicity. J. Appl. Anal., 27(1):153–162, 2021. https://doi.org/10.1515/jaa-2020-2041
E. Azroul and F. Balaadich. A weak solution to quasilinear elliptic problems with perturbed gradient. Rend. Circ. Mat. Palermo II, 70:151–166, 2021. https://doi.org/10.1007/s12215-020-00488-4
J.M. Ball. A version of the fundamental theorem for Young measures. In M. Rascle, D. Serre and M. Slemrod(Eds.), PDEs and Continuum Models of Phase Transitions, volume 344, pp. 207–215, Berlin, Heidelberg, 1989. Springer Berlin Heidelberg. https://doi.org/10.1007/BFb0024945
V. Bo¨gelein, F. Duzaar, L. Scha¨tzler and C. Scheven. Existence for evolutionary problems with linear growth by stability methods. J. Differential Equations, 266(11):7709–7748, 2019. https://doi.org/10.1016/j.jde.2018.12.012
M. Caddick and E. Suli. Numerical approximation of Youngmeasure solutions to parabolic systems of forward-backward type. Applicable Analysis and Discrete Mathematics, 13(3):649–696, 2019. https://doi.org/10.2298/AADM190325026C
S. Demoulini. Young measure solutions for a nonlinear parabolic equation of forward-backward type. SIAM Journal on Mathematical Analysis, 27(2):376– 403, 1994. https://doi.org/10.1137/S0036141094261847
G. Dolzmann, N. Hungerbühler and S. Müller. Nonlinear elliptic systems with measure-valued right hand side. Mathematische zeitschrift, 226:545–574, 1997. https://doi.org/10.1007/PL00004354
L.C. Evans. Weak convergence methods for nonlinear partial differential equations. CBMS Reg. Conf. Ser. in Math., 74, 1990. https://doi.org/10.1090/cbms/074
N. Hungerbühler. A refinement of Ball’s theorem on Young measures. New York J. Math, 3:48–53, 1997.
N. Hungerbühler. Quasilinear elliptic systems in divergence form with weak monotonicity. New York J. Math., 5:83–90, 1999.
N. Hungerbühler. Quasilinear parabolic systems in divergence form with weak monotonicity. Duke mathematical journal, 107(3):497–519, 2001. https://doi.org/10.1215/S0012-7094-01-10733-3
E. Kamke. Das Lebesgue-Stieltjes-Integral. Teubner, Leipzig, 1960.
G.M. Lieberman. The natural generalizationj of the natural conditions of Ladyzhenskaya and Ural’tseva for elliptic equations. Communications in Partial Differential Equations, 16(2-3):311–361, 1991. https://doi.org/10.1080/03605309108820761
P. Marcellini. A variational approach to parabolic equations under general and p, q-growth conditions. Nonlinear Analysis, 194:111–456, 2020. https://doi.org/10.1016/j.na.2019.02.010
R. Di Nardo, F. Feo and O. Guibe. Existence result for nonlinear parabolic equations with lower order terms. Anal. Appl.(Singap.), 9(2):161–186, 2011. https://doi.org/10.1142/S0219530511001790